L’impact du Big Data sur les modèles de crédit : révolution ou évolution ?

Le Big Data est une expression anglophone désignant un ensemble des données volumineux qui se caractérise, généralement, par les 3V :

• la vélocité : la vitesse à laquelle les données sont collectées et traitées ;
• la variété : l’origine variée des sources de données ;
• le volume des données collectées, qui atteint les petaoctets (10¹⁵ octets).

Cette notion est vue comme la révolution industrielle du XXI ^e siècle qui va impacter toutes les entreprises, tous secteurs d’activité confondus, et dans de nombreux domaines, que ce soit le marketing, la détection de fraude ou encore la maîtrise du risque. Mais les avis sont partagés, notamment en ce qui concerne l’impact sur les modèles de risque de crédit ; certains acteurs pensent que le Big Data va révolutionner la statistique, tandis que d’autres ne voient dans le Big Data qu’une évolution du data mining et de l’analyse de données. Pour répondre aux différentes questions, des retours d’expérience seront nécessaires.

Le Big Data : véritable révolution technologique

Le volume et la variété de l’information disponible vont permettre d’enrichir considérablement la connaissance du client, de pouvoir créer des profils de risque en fonction de ses goûts, de son réseau social. L’entreprise pourra étudier une source inépuisable de données, en temps quasi réel. L’individu ne sera plus vu de manière isolée, mais en tant qu’élément d’un groupe formant un réseau.

L’entreprise pourra analyser des centaines, voire des milliers de dimensions, afin d’optimiser et identifier les performances des modèles de crédit. La vitesse de mise à jour des données, parfois en temps réel, est une excellente aide pour la maîtrise du risque et la prise de décision.

Mais un travail important devra être fait en amont sur la méthodologie à employer pour traiter des informations, dont le format est différent du format standard (textes et chiffres), comme les images, les vidéos ou encore les mails.

La variété des sources pourra également permettre à l’entreprise d’améliorer la qualité et la fiabilité de ses données en comparant les différentes sources entre elles, de vérifier la cohérence des informations obtenues lors de la demande de prêt, mais à la condition que les données ainsi collectées soient correctement intégrées à la base de données. En effet, les données issues de la toile seront en grande partie non structurées, car elles auront potentiellement un nombre de valeurs toutes différentes et impossibles à catégoriser. Pour leur exploitation, elles devront être structurées. Dans le cas où les données sont mal intégrées, l’entreprise risque de se « noyer » sous un flot d’informations qu’elle ne sera pas capable de restituer et valoriser correctement.

La véracité des informations issues des réseaux sociaux tels que Facebook ou Viadeo sera à contrôler. En effet, n’importe quelle personne peut indiquer ce qu’elle souhaite. Des informations issues de sites comme Viadeo et Linkedin seront plus facilement vérifiables, avec les bulletins de salaire par exemple.

Avec l’augmentation considérable du volume de données, le statisticien n’aura plus le temps d’étudier les variables une à une. Il devra d'abord faire du traitement de masse, puis analyser les variables qui ressortent comme discriminantes. Au vu de la multitude de données disponibles, des compétences métier seront nécessaires, afin de mieux cibler les variables ou croisement de variables pouvant aider à la prédiction du critère de défaut, ou non-défaut.

De même, les méthodes statistiques usuelles, comme la régression logistique [1] , les arbres de décision ou encore les réseaux de neurones, ne gèrent pas les valeurs manquantes, ce qui va demander une étude approfondie des raisons de l’absence de ces informations.

De plus, la régression logistique [2] est très sensible au problème de multi-colinéarité partielle, qui se manifeste lorsqu’une variable explicative est fortement corrélée à une ou plusieurs variables explicatives (ou à l’une de leur combinaison). Lorsque ce problème est rencontré, on observe souvent :

• une forte variance [3] des pondérations estimées et d'importants intervalles de confiance [4] autour des pondérations ;
• les tests de Wald, qui testent la nullité de chaque pondération, non rejetés, bien que les variables explicatives concernées soient significatives vis-à-vis du défaut ;
• des pondérations estimées de signes contraires au risque de défaut ;
• des variables qui entrent dans le modèle alors que ça ne devrait pas être le cas.

Tester de multiples modèles

Pour pallier ce problème, un travail considérable, en amont, de l'étude des liaisons entre les différentes variables explicatives est exigé et de multiples modèles doivent être testés, en excluant une ou plusieurs variables explicatives concernées par le problème de multicolinéarité.

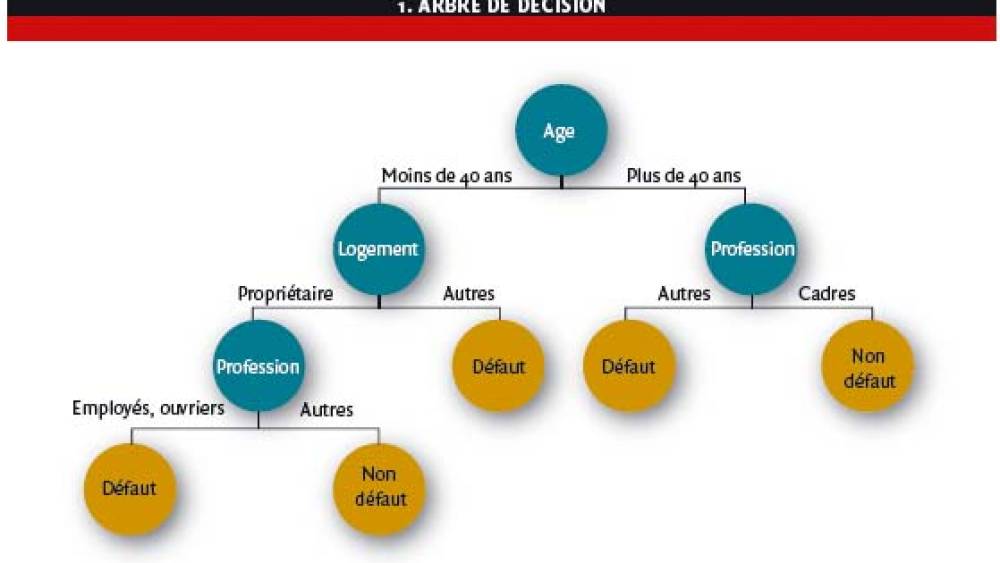
L’arbre de décision (voir Figure 1) est une méthode de segmentation représentée graphiquement comme un arbre, composé de nœuds de décision (les ronds foncés) reliés par des branches et de nœud terminaux (ronds clairs) qui donnent la décision finale. C’est une méthode statistique peu robuste en présence d’un grand nombre de variables. En effet, plus il y a de variables en entrée, plus le nombre de test de modèle augmente. Un mauvais choix de variable au début peut conduire à un arbre avec un faible pouvoir discriminant.

De plus, si l’arbre de décision est fait sur des variables qualitatives alors le temps de traitement augmente avec le nombre de modalités des variables. Et si l’arbre de décision est établi sur des variables quantitatives, alors il choisit le seuil de découpage de la variable et risque de construire des classes trop petites.

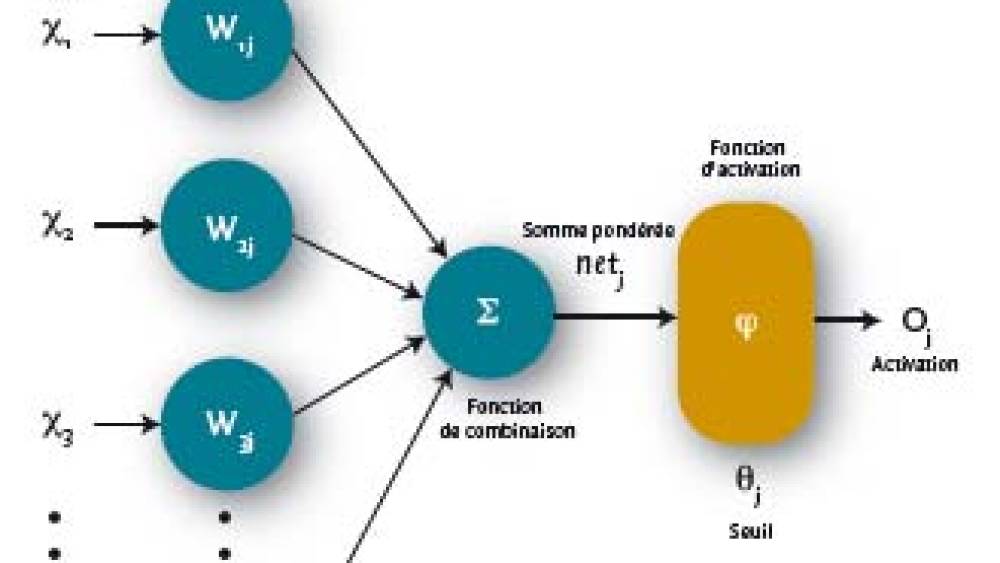
Le réseau de neurones (voir Encadré 3) est une méthode statistique d’apprentissage supervisé inspirée du fonctionnement du cerveau humain. Il est composé de plusieurs neurones. À chaque entrée de neurone, correspondent n variables notées x_i (i  [1 ; n]) à laquelle on affecte un poids (w_ij), pour le j^e neurone. Une combinaison linéaire entre les variables d’entrée et les poids est effectuée, ce qu’on appelle somme pondérée. Cette somme pondérée (souvent égal à la _jx_i * w_ij) est soumise à une fonction d’activation (linéaire par exemple) déterminée en fonction du seuil _j. En sortie de la fonction d’activation, un paramètre de sortie (o_j) est transmis à un autre neurone comme paramètre d’entrée.

Les réseaux de neurones sont composés de trois couches :

• la première couche, dite d’entrée, reçoit les données sources ; sa taille est directement impactée par le nombre de variables en entrée (les variables explicatives) ;
• la seconde, cachée, n’a pas de contact avec « l’extérieur » ;
• la couche de sortie donne le résultat final, ici le défaut ou non.

Cette méthode a de nombreux inconvénients, en plus de sa non-gérance des valeurs manquantes, comme l’initialisation des poids du réseau ou encore le choix du nombre de neurones dans la couche cachée qui demande de tester plusieurs tailles possibles afin d’obtenir de bons résultats. Il existe de surcroît un risque de sur-apprentissage (ou d’apprentissage « par cœur ») lorsque le modèle comporte trop de variables explicatives, car il expliquera les résidus au lieu du comportement global.

Les limites des modèles actuels vont exiger du statisticien de trouver d’autres méthodes de scoring.

Le Big Data comme simple évolution du data mining et de l’analyse de données

Souvent, le Big Data est vu comme une véritable révolution, car le volume de données est impressionnant et les formats de données nouveaux. Or les mathématiques prennent déjà en compte des tailles et dimensions infinies pour les modèles de conception hilbertien.

Une première solution est la régression logistique PLS [5] , issue de la régression des moindres carrés partiels inventée en 1983 par Svante et Herman Wold. Elle est principalement utilisée en biologie, pour l’expression des gènes, où les données sont fortement corrélées entre elles. Cette méthode est réputée pour être une bonne solution au problème de multi-colinéarité, qui gère les valeurs manquantes et qui tolère très bien les situations où les variables sont beaucoup plus nombreuses que les observations (voir Encadré 1).

Une deuxième solution est d’utiliser le Séparateur à Vaste Marge ou Support Vector Machine (SVM), utilisé en bio-informatique. Cette méthode découle directement des travaux en théorie de l’apprentissage de Vapnik, à partir de 1995. Elle a été définie à l’origine pour la prévision d’une variable dichotomique (0 ou 1). Elle est basée sur la recherche de l’hyperplan de marge optimale qui, lorsque c’est possible, classe ou sépare correctement les données en deux groupes : défaut et non-défaut, tout en étant le plus éloigné possible de toutes les observations. Le but étant de minimiser le nombre d’observations mal classées à l’aide d’un classifieur, ou fonction de décision. Le modèle SVM peut être linéaire si les données sont linéairement séparables. Dans le cas où les données sont non séparables, la solution consiste à modéliser des erreurs potentielles par des variables d’écart positives pour utiliser le modèle SVM linéaire. Mais, en pratique, la frontière optimale n’est pas linéaire ; des noyaux vont donc être introduits dans le modèle. Les méthodes à noyaux ont l’avantage d’être très flexibles pour s’adapter à des objets complexes comme des images, des vidéos ou encore des graphes. De plus, sur le plan algorithmique, les algorithmes sont moins pénalisés par le nombre de variables que par le nombre d’individus. À noter que les noyaux ont été introduits dans la statistique dès les années 1950. Leur principal inconvénient réside dans leur complexité.

Une troisième alternative aux méthodes usuelles est l’utilisation du réseau bayésien [6] . Cette méthode a été initiée par Judea Pearl dans les années 1980. Elle permet de traiter de grands jeux de données afin d’en extraire des connaissances utiles à la prise de décision, de prévoir ou contrôler le comportement d’un emprunteur, par exemple (voir Encadré 4).

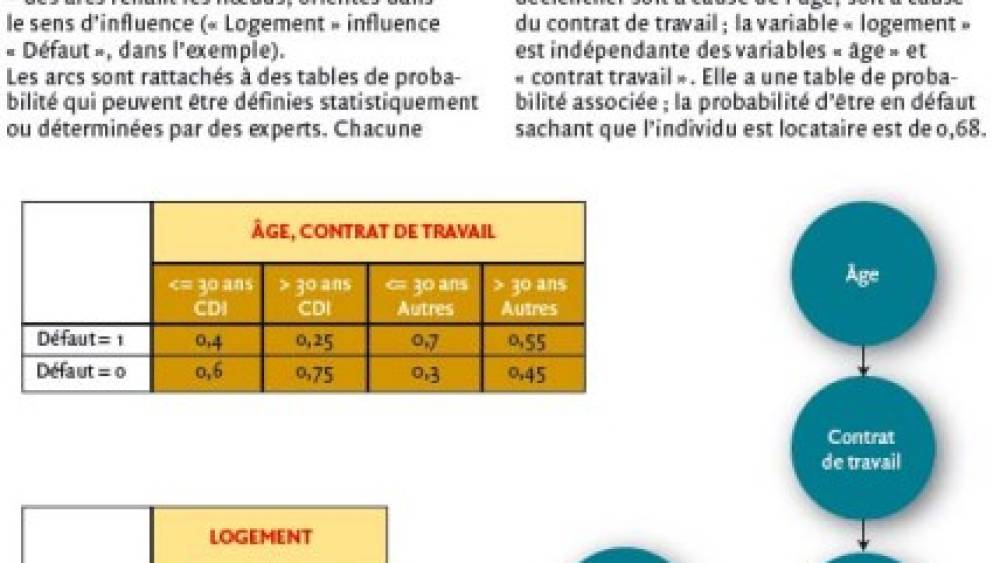
L’avantage de cette méthode est son fort pouvoir discriminant, qu’elles s’utilisent aussi bien sur des variables qualitatives et quantitatives et prend en compte leurs incertitudes. Elle est très pratique pour la représentation de connaissances incertaines et le raisonnement à partir d’informations incomplètes, et permet ainsi d’intégrer de nouvelles informations comme l’expertise ou encore le retour d’expérience. Les réseaux bayésiens ont l’avantage, par son graphique, d’être une méthode intuitive qui permet de voir les dépendances entre les variables et qui aide à comprendre le modèle.

Un avantage concurrentiel

Que le Big Data soit une révolution ou une simple évolution, tous les auteurs s’accordent à dire que l’entreprise qui résoudra les différentes problématiques – mathématique, informatique et métier – tirera du Big Data un avantage concurrentiel considérable.

1 La régression logistique est une méthode statistique qui s’utilise lorsque l’on cherche à expliquer la survenue d’un événement (par ex. le défaut de paiement) à l’aide de variables explicatives (pouvant être continues ou discrètes) susceptibles d’influencer la survenue de cet événement (par ex. l’âge). 2 Gilbert Saporta, Probabilités, analyse des données et statistique, Éditions Technip, 2006. 3 La variance est un outil statistique qui permet de mesurer la dispersion d'une variable par rapport à sa moyenne. 4 L'intervalle de confiance permet d'évaluer la précision de l'estimation d'un paramètre statistique sur un échantillon. 5 Christophe Croux, Jean-Jacques Droesbeke, Pierre-Louis Gonzalez, Christian Gourieroux, Gentiane Haesbroeck, Michel Lejeune, Gilbert Saporta et Michel Tenenhaus, Modèles statistiques pour données qualitatives, Éditions Technip, 2005. 6 Patrick Naïm, Pierre-Henri Wuillemin, Philippe Leray, Olivier Pourret et Anna Becker, Réseaux bayésiens, Éditions Eyrolles (2007).